P-values and Posterior Probabilities

You might want to argue that the question in the subtitle is based on a false premise; the p-value is related to the probability of falsely rejecting the null hypothesis conditional on the level ($\alpha$) and the null hypothesis being true. The question of whether the null-model valid or not is only assessed from this viewpoint and we certainly cannot assign a probability it.

However in Bayesian statistics such a question is perfectly valid. The theory of Bayesian robustness examines how sensitive a Bayesian inference is to the choice of prior. Thereby addressing one of the main criticisms of Bayesian statistics. In a seminal paper, James O. Berger and Thomas Sellke consider a single realization (the results still holds for multiple realizations) of a normal variable with known variance:

and a test for the hypothesis

against the alternative

Let’s also phrase a Bayesian model; we give each of the two models an equal prior probability $P(M_0)=\frac{1}{2}.$ We also need a prior for $\theta$ under $M_1$, $g(\theta)$. Berger and Sellke shows that if $|X| > 1$ corresponding to a p-value less than 0.32, the prior favoring $M_1$ the most within the class of symmetric unimodal distributions is a uniform distribution,

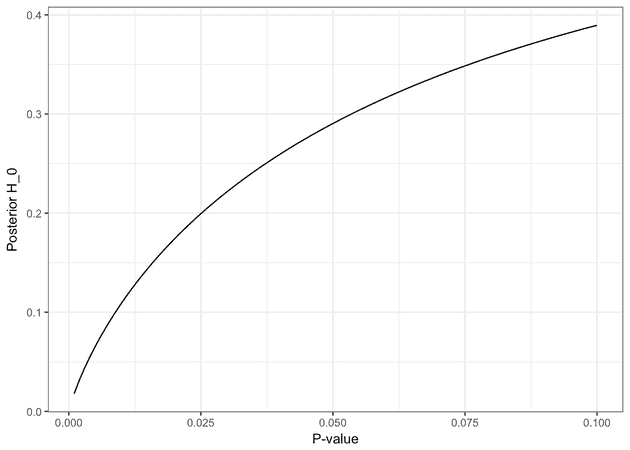
We find the $K$ that maximizes the posterior probability of the alternative for different values of $X$ and their corresponding posterior probabilities and p-values.

P-value	Posterior of H0
0.100	0.3895459
0.050	0.2904357
0.010	0.1094489
0.001	0.0177166

This answers our question: With the prior that favors the alternative the most the posterior probability that the null hypothesis is true for a p-value of 0.045 is still 0.28. Not exactly overwhelming evidence for the alternative.

Below we have plotted the posterior probability for $H_0$ against the p-value for the prior that favors the alternative the most.